The Mandelbrot Set
The most well-known fractal object is probably the Mandelbrot Set, named for Benoit Mandelbrot, who first investigated its fractal properties in the late 1970s. Unlike some of my own algorithms, the Mandelbrot set takes a lot of time to compute.
The Algorithm
Each complex number can be considered as a point on the plane. Imagine that you take such a number, square it, add it to itself, then square the new number, add it to itself, and repeat the process indefinitely. The resulting sequence of points will either converge towards a limit point, or diverge - the numbers get larger and larger. If they converge, the original point is considered to be in the Mandelbrot set.
When the computer calculates, it tests each point by following the above process. It can never be certain that a point is in the set, so it will stop after a certain number of repetitions and declare the point to be part of the set. If the calculated number passes a certain threshold (an absolute magnitude of 2) then the point cannot possibly be in the set, and is "thrown out".
In the Mandelbrot images, points in the set are shown as black areas. The interesting parts of the images are the points which are not in the set. They are assigned different colors according to how quickly they diverge - that is, how many repeated calculations have occurred before the point is "thrown out".
Zooming in on the Maps
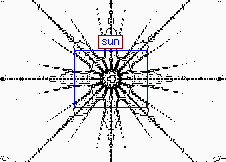
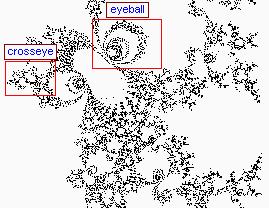
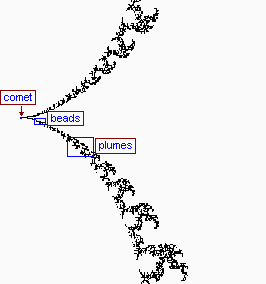
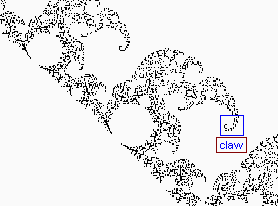
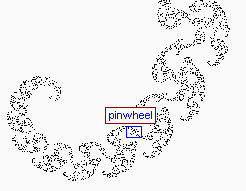
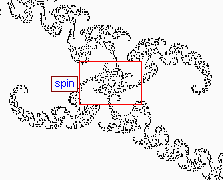
I have assigned arbitrary names to the images according to aspects of their appearance. Each named section features a monochrome map of the area, with rectangles showing further zooms which you may investigate. If you click on a blue rectangle, you will zoom further and be shown to another map. If you click on a red rectangle, you will see the expanded color image itself, since no further zooming in on that area is allowed.
If you click any of the thumbnail images, you will see an enlarged color image of the same area.
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
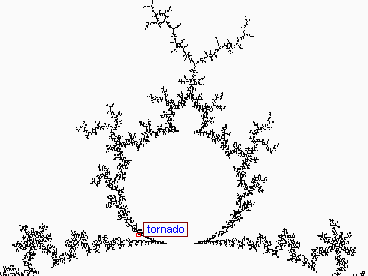
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
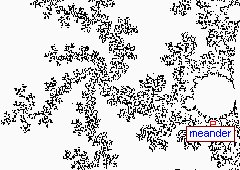
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
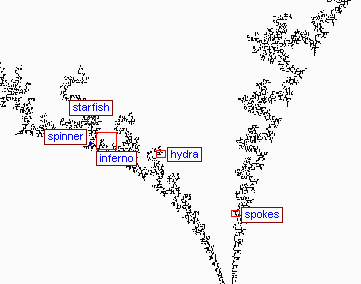
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
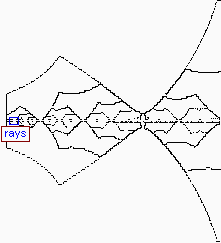
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|

|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
Click the blue rectangles to zoom further (red rectangles indicate that no further zooming is possible). Click a thumbnail for the image itself.
-----------------------------
|
|
Back to Top of Page Back to Fractals Page
The Mandelbrot Set
Last Updated October 6th, 2001
Web Page by Ned May
URL http://chromatism.net/chromat/mandelb.htm
All images and text are ©2017 by Edward S. May unless otherwise noted. All rights reserved.
























































